День второй - анализ данных¶

В сегодняшнем дне мы погрузимся в аналитику данных как таковую, и нас ждут следующие блоки:

библиотеки работы с данными numpy, pandas, pyplot, seaborn, ipywidgets,
понятие разведочного анализа и предобработки признаков. поймем, почему нельзя полагаться только на выборочные статистики как числа,
линейные модели и градиентный спуск,
деревья решений и ансамбли моделей на основе деревьев решений,
алгоритм ближайших соседей и соседство как таковое (весьма важно на практике), в том числе на примерах текстовых данных,
(пока) поверхностно: нейронные сети в библиотеке scikit-learn.

2.1 Библиотеки работы с данными¶

Библиотеки numpy и pandas¶

Библиотека numpy предназначена для работы с многомерными массивами. Мы уже видели примеры в первом дне, как ей можно пользоваться, теперь чуть-чуть поподробнее на примерах.

# запретим предупреждения
import warnings
warnings.filterwarnings('ignore')

import numpy as np # общепринятое сокращение

# создадим первый numpy-массив.
# каждый элемент первого уровня содержит другой массив... 
# второй уровень - числа

array = np.array([[1, 2], [3, 4]])
array

array([[1, 2],
       [3, 4]])

# с массивами numpy можно проделывать различные операции одновременно надо всеми элементами

# в квадрат и минус 1
array ** 2 - 1

array([[ 0,  3],
       [ 8, 15]], dtype=int32)

# все массивы numpy должны иметь одинаковый тип элементов

array.dtype, array.astype(float).dtype

(dtype('int32'), dtype('float64'))

# библиотека numpy содержит множество полезных функций

np.log(np.e), np.allclose(0, np.sin(np.pi))

(1.0, True)

# массивы numpy можно индексировать вот так

# первая строка, вторая колонка
array[0, 1]

# вся вторая колонка
array[:, 1], "эквивалентно", array[None:None, 1]

(array([2, 4]), 'эквивалентно', array([2, 4]))

# есть полезные операции над массивами, например среднее

# среднее по всем элементам, среднее по каждому столбцу (по вертикали), среднее по каждой строке (по горизонтали)
array.mean(), array.mean(axis=0), array.mean(axis=1)

(2.5, array([2., 3.]), array([1.5, 3.5]))

# преобразовать размерность массива
# - первое - чтобы была одна колонка
# - второе - чтобы была одна строка

array.reshape(-1, 1), array.reshape(1, -1)

(array([[1],
        [2],
        [3],
        [4]]),
 array([[1, 2, 3, 4]]))

Нам часто будет нужен метод .reshape, так как он может полезен при конвертации данных в массивы, пригодные для обучения моделей. Если на одной какой-то оси стоит -1, то количество элементов на ней будет рассчитано автоматически. Так например, .reshape(-1, number_of_features) - сделает массив с количеством примеров, каждая строка которого - список признаков.

По сути, массивы numpy - это те же “числа”, с точки зрения операций. Однако благодаря еще наличию в них структуры - набор этих операций шире.

Далее. Библиотека pandas в свою очередь предназначена для работы с табличными данными, и колонки таблицы могут иметь разный тип. Давайте рассмотрим датасет, на котором мы будем дальше часто тренироваться - датасет Abalone (ракушки).

Это датасет физических замеров ракушек, с различными признаками. Нужно предсказывать возраст ракушки по физическим параметрам. Делается это путем подсчета колец, но это достаточно долгая и нудная процедура, причем с применением микроскопа - да и ракушку надо пилить. Добавив 1.5 к количеству колец (зависит правда от локации) - обычно получают возраст.

Мы будем по-разному формулировать задачи с этим датасетом, но пока это неважно. Давайте на него посмотрим.

# подключим pandas с общепринятым сокращением
import pandas as pd

dataframe = pd.read_csv(
    'data/abalone.csv', 
    sep=',', # что является разделителем колонок в файле,
    decimal='.', # что является разделителем десятичных дробей в записи чисел
    parse_dates=[], # мы знаем, что дат у нас нет, если бы они были, здесь можно было бы перечислить колонки
    header=0 # названия колонок в первой строке
)

# посмотрим на случайные 15 записей
dataframe.sample(15)

	sex	length	diameter	height	whole weight	shucked weight	viscera weight	shell weight	rings
797	M	0.440	0.335	0.110	0.3940	0.1570	0.0960	0.1220	9
66	F	0.565	0.440	0.160	0.9150	0.3540	0.1935	0.3200	12
2480	F	0.520	0.425	0.145	0.7000	0.2070	0.1905	0.2400	13
4062	M	0.630	0.490	0.150	1.1955	0.5845	0.2570	0.3000	9
913	I	0.370	0.290	0.095	0.2490	0.1045	0.0580	0.0670	6
792	M	0.470	0.370	0.180	0.5100	0.1915	0.1285	0.1625	9
405	F	0.525	0.440	0.150	0.8425	0.3685	0.1985	0.2400	12
531	F	0.460	0.355	0.130	0.4580	0.1920	0.1055	0.1300	13
2383	F	0.525	0.390	0.135	0.6005	0.2265	0.1310	0.2100	16
3720	F	0.380	0.320	0.115	0.6475	0.3230	0.1325	0.1640	7
3313	M	0.400	0.310	0.110	0.3140	0.1380	0.0570	0.1000	11
3390	M	0.560	0.440	0.160	1.1115	0.5035	0.2785	0.2600	10
2080	M	0.645	0.495	0.150	1.2095	0.6030	0.2225	0.3390	9
3417	M	0.580	0.460	0.150	1.0165	0.4910	0.2210	0.2650	9
1447	M	0.440	0.320	0.120	0.4565	0.2435	0.0920	0.1025	8

Здесь у нас есть поля пола (M - мужской, F - женский и I - дети), есть поля длины, диаметра, высоты - в мм, четыре разных веса (полный и веса по составляющим) в граммах, и количество колец (целое число).

Давайте посмотрим, как можно работать с такой таблицей.

# описательные статистики для числовых полей

dataframe.describe()

	length	diameter	height	whole weight	shucked weight	viscera weight	shell weight	rings
count	4177.000000	4177.000000	4177.000000	4177.000000	4177.000000	4177.000000	4177.000000	4177.000000
mean	0.523992	0.407881	0.139516	0.828742	0.359367	0.180594	0.238831	9.933684
std	0.120093	0.099240	0.041827	0.490389	0.221963	0.109614	0.139203	3.224169
min	0.075000	0.055000	0.000000	0.002000	0.001000	0.000500	0.001500	1.000000
25%	0.450000	0.350000	0.115000	0.441500	0.186000	0.093500	0.130000	8.000000
50%	0.545000	0.425000	0.140000	0.799500	0.336000	0.171000	0.234000	9.000000
75%	0.615000	0.480000	0.165000	1.153000	0.502000	0.253000	0.329000	11.000000
max	0.815000	0.650000	1.130000	2.825500	1.488000	0.760000	1.005000	29.000000

# количество ракушек разных полов

dataframe.groupby('sex')['rings'].count()

sex
F    1307
I    1342
M    1528
Name: rings, dtype: int64

# количество ракушек по полам, в случае если диаметр ракушки больше среднего

dataframe[dataframe.diameter > dataframe.diameter.mean()].groupby('sex')['rings'].count()

sex
F     988
I     256
M    1070
Name: rings, dtype: int64

Уже сейчас по числам видно, что маленький диаметр ракушки - это преимущественно дети.

# срез данных по колонкам и строкам
# первая и последние колонки и последние три строки

dataframe[['sex', 'rings']][-3:]

	sex	rings
4174	M	9
4175	F	10
4176	M	12

# сортировка датасета - и посмотрим максимальный
# .values - это получить колонку как numpy-массив

dataframe.sort_values('rings').rings.values[-1] # ракушка-старожил

# каждый датафрейм (объект таблицы) имеет индекс

dataframe.index[:4:2]

RangeIndex(start=0, stop=4, step=2)

# получить записи по индексу таблицы, и выборочно колонки

dataframe.loc[dataframe.index[:4:2]][dataframe.columns[:3]]

	sex	length	diameter
0	M	0.455	0.365
2	F	0.530	0.420

Таблицы pandas можно так же склеивать (по горизонтали и вертикали), делать агрегированные (сводные) таблицы, и многое другое.

Библиотеки визуализации¶

Мы посмотрим на две - первая это matplotlib - универсальная, вторая, это надстройка над ней под названием seaborn - очень удобная для визуализации в статистических исследованиях.

%matplotlib inline
# важная строка, если надо чтобы диаграммы выводились в тетрадке
# она должна быть раньше всех, прежде чем что-то рисовать

import matplotlib.pyplot as plt # тоже общепринятое сокращение

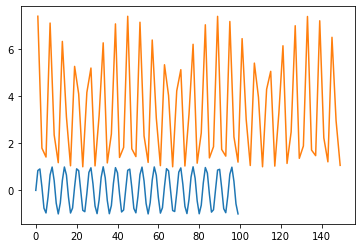
# наша первая линейная диаграмма
plt.plot(np.sin(range(100))); # точка с запятой нужна, чтобы не выводить в тетрадку запись об объекте

# наша вторая диаграмма, она наложится
plt.plot(range(1, 151, 2), np.exp(np.cos(range(0, 150, 2)) + 1));

# на тот случай, если мы хотим изображение больше
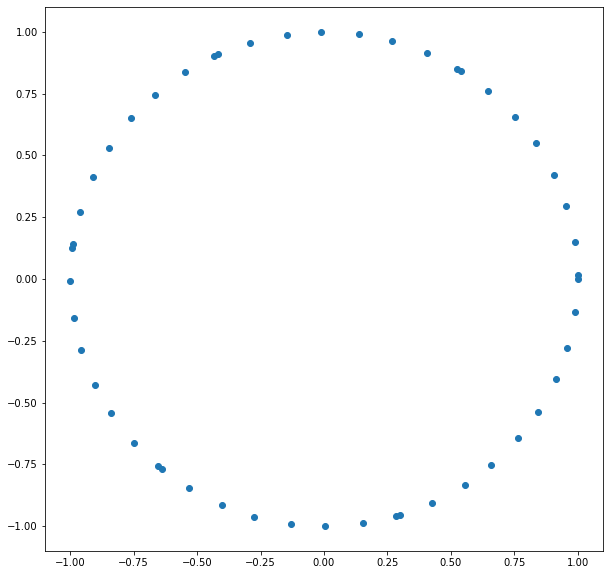
plt.figure(figsize=(10, 10)) # длина и высота... в дюймах!

# точечная диаграмма
plt.scatter(np.cos(range(50)), np.sin(range(50)));

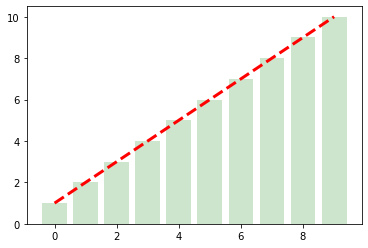
# диаграммы можно накладывать друг на друга даже когда они разных типов

plt.bar(
    range(10), # значения на оси абсцис
    np.linspace(1, 10, 10), # высота столбцов
    color='green', # понятно, цвет
    alpha=0.2 # прозрачность
);

plt.plot(
    range(10), # значения x
    np.linspace(1, 10, 10), # значения y
    color='red', # тут тоже понятно
    ls='--', # стиль линии
    lw=3 # ширина линии
);

Библиотека seaborn содержит очень много полезных способов визуализации данных, лучше всего их посмотреть в галерее библиотеки. Нас же будут интересовать три:

Как построить график распределения какой-либо величины,
Попарные точечные диаграммы,
График серий.

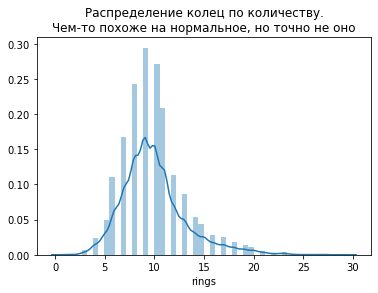
# посмотрим на распределение колец ракушек
import seaborn as sns

plt.title("Распределение колец по количеству.\nЧем-то похоже на нормальное, но точно не оно")
sns.distplot(dataframe.rings);

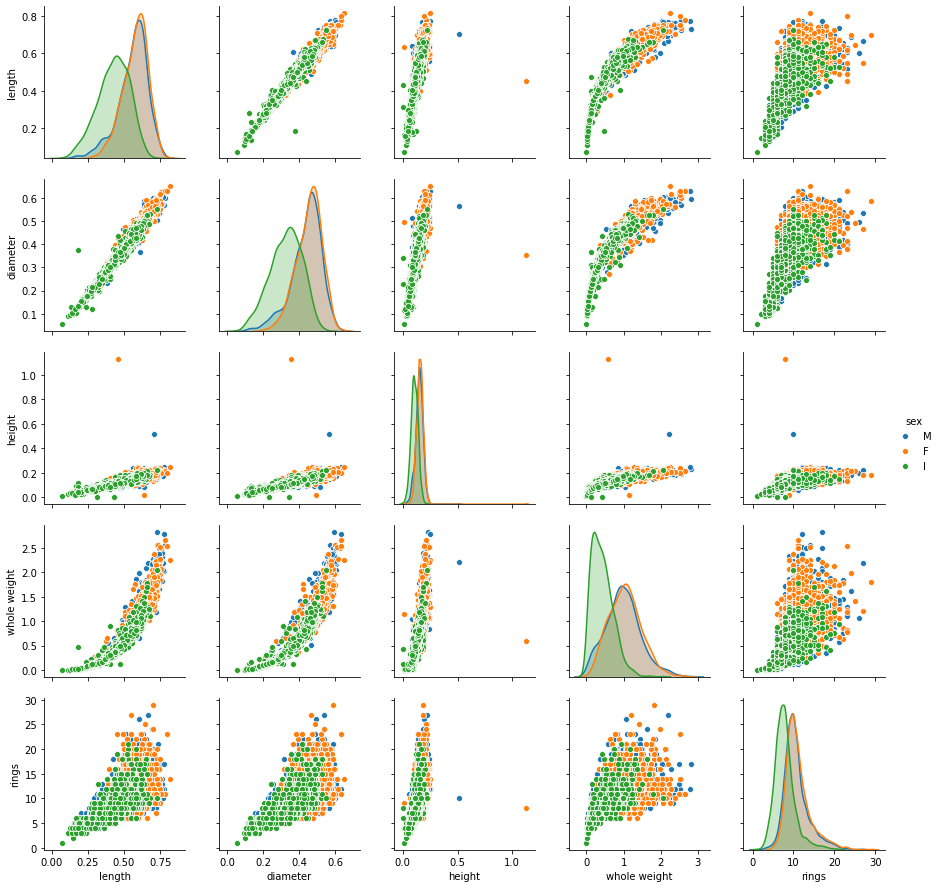
# попарные точечных диаграммы

sns.pairplot(data=dataframe[['length', 'diameter', 'height', 'whole weight', 'rings', 'sex']], hue='sex');

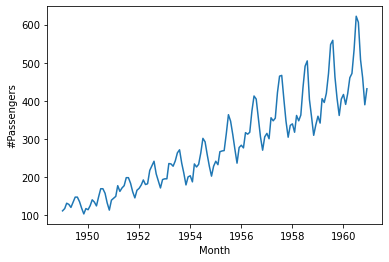
# и наконец, диаграмма серий (пример с датами)

airpassengers = pd.read_csv('data/airpassengers.csv', parse_dates=['Month'])
sns.lineplot(x="Month", y="#Passengers", data=airpassengers);

А теперь - интерактив!¶

Досточно легко сделаем наши диаграммы интерактивными в ноутбуках с помощью ipywidgets.

from ipywidgets import interact

def draw_function(length):
    sns.lineplot(x="Month", y="#Passengers", data=airpassengers[:length]);
    
interact(
    draw_function,
    length=(
        12, # минимальное значение
        len(airpassengers), # максимальное
        12 # шаг
    )
);

В библиотеке ipywidgets много всяких полезностей, тем не менее подробно мы на них не будем останавливаться. Метод interact автоматически распознаёт тип переменной, и подставит - для строки поле ввода текста, для числа с плавающей запятой - слайдер, и так далее.

2.2 Разведочный анализ и препроцессинг¶

Разведочный анализ, или понимание данных - важный этап, который может сократить большое количество времени. Давайте сразу посмотрим на квартет Энскомба (Anscombe’s quartet). Это четыре набора данных, каждый из которых линейно аппроксимируется одинаково.

quartet = pd.read_csv('data/anscombes.csv').drop('id', axis='columns')

plt.figure(figsize=(10, 10))
for index, dataset in enumerate(['I', 'II', 'III', 'IV']):
    plt.subplot(2, 2, index + 1)
    plt.scatter(
        quartet[quartet.dataset == dataset].x,
        quartet[quartet.dataset == dataset].y,
        c=['blue', 'green', 'red', 'black'][index]
    );
    plt.xlim(0, 20);
    plt.ylim(0, 20);

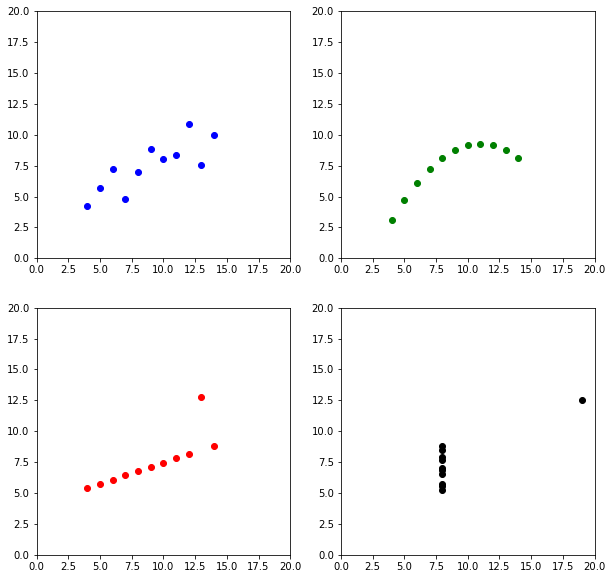
Это четыре разных датасета, но посмотрим их статистики.

quartet.groupby('dataset').describe().T 

	dataset	I	II	III	IV
x	count	11.000000	11.000000	11.000000	11.000000
	mean	9.000000	9.000000	9.000000	9.000000
	std	3.316625	3.316625	3.316625	3.316625
	min	4.000000	4.000000	4.000000	8.000000
	25%	6.500000	6.500000	6.500000	8.000000
	50%	9.000000	9.000000	9.000000	8.000000
	75%	11.500000	11.500000	11.500000	8.000000
	max	14.000000	14.000000	14.000000	19.000000
y	count	11.000000	11.000000	11.000000	11.000000
	mean	7.500909	7.500909	7.500000	7.500909
	std	2.031568	2.031657	2.030424	2.030579
	min	4.260000	3.100000	5.390000	5.250000
	25%	6.315000	6.695000	6.250000	6.170000
	50%	7.580000	8.140000	7.110000	7.040000
	75%	8.570000	8.950000	7.980000	8.190000
	max	10.840000	9.260000	12.740000	12.500000

Как видим, количество, среднее и разброс у всех наборов одинаковый! В частности, линейные алгоритмы только на это и полагаются. Поэтому очень ВАЖНО смотреть попарные диаграмми глазами.

from sklearn.linear_model import LinearRegression

coefs = []

plt.figure(figsize=(10, 10))
for index, dataset in enumerate(['I', 'II', 'III', 'IV']):
    plt.subplot(2, 2, index + 1)
    plt.scatter(
        quartet[quartet.dataset == dataset].x,
        quartet[quartet.dataset == dataset].y,
        c=['blue', 'green', 'red', 'black'][index]
    );
    model = LinearRegression().fit(
        quartet[quartet.dataset == dataset].x.values.reshape(-1, 1),
        quartet[quartet.dataset == dataset].y
    ) # y = kx + b
    coefs.append([
        model.coef_[0], # это k
        model.intercept_ # это b
    ])
    line = model.predict(quartet[
        quartet.dataset == dataset
    ].x.values.reshape(-1, 1))
    plt.plot(
        quartet[quartet.dataset == dataset].x,
        line,
        ls='-.',
        c='orange',
        lw=1
    )
    plt.xlim(0, 20);
    plt.ylim(0, 20);

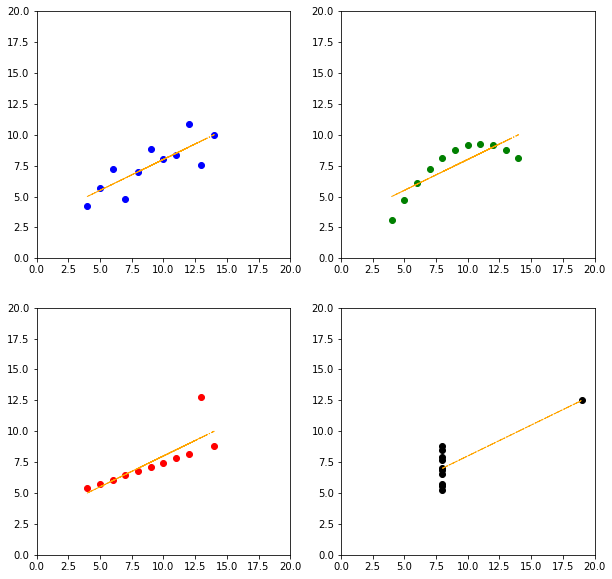
np.array(coefs)[:, 0], np.array(coefs)[:, 1]

(array([0.50009091, 0.5       , 0.49972727, 0.49990909]),
 array([3.00009091, 3.00090909, 3.00245455, 3.00172727]))

Коэффициенты практически одинаковые.

Так что же представляет собой разведочный анализ? Давайте остановися на том, что это не просто подсчет описательных статистик (сколько, среднее, разброс), но и построение диаграмм, на которых можно уловить какие-то зависимости, возможно даже глазами.

sns.pairplot(dataframe[['whole weight', 'diameter', 'sex']], hue='sex');

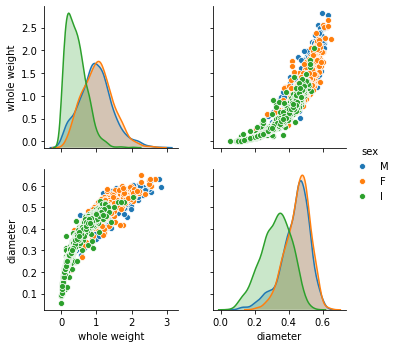
Здесь мы видим некоторую изогнутую зависимость между весом ракушки и её диаметром. Может она степенная? Мы можем предположить, что извлечение квадратного корня “исправит ситуацию”, и может превратить зависимость в линейную. Проверим хотя бы визуально, без метрик.

dataframe_copy = dataframe.copy()
dataframe_copy['root_weight'] = np.sqrt(dataframe_copy['whole weight'])
sns.pairplot(dataframe_copy[['root_weight', 'diameter', 'sex']], hue='sex');

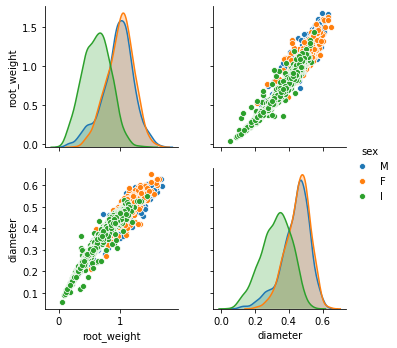
Как видим, мы слегка “выпрямили” зависимость, хотя и не до конца (это означает что степень на самом деле еще меньше одной второй). А то, что мы процедурно сделали, называется feature engineering - преобразование признаков, с целью подогнать данные под линейную модель (которая хорошо работает с прямолинейными зависимостями).

# попробуем с третьей степенью

dataframe_copy['changed_weight'] = np.power(dataframe_copy['whole weight'], 1 / 3)
sns.pairplot(dataframe_copy[['changed_weight', 'diameter', 'sex']], hue='sex');

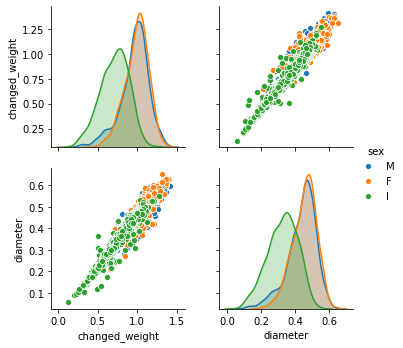
Можно сказать угадали. Но на самом деле, эти подсказки могут давать не только сами данные, но и их практический смысл. В данном случае, вес ракушки пропорционален диаметру в третьей степени. Почему? Потому что вес пропорционален объему, а объем (например шара) - пропорционален третьей степени диаметра.

Поэтому feature engineering полагается скорее на зависимости в данных, которые известны (или их можно предположить) независимо от этих самых данных.

Забегая вперед - нейросети часто могут сами делать feature engineering. Поэтому они получили такую популярность. Но нам надо и без этого самим уметь!

Препроцессинг - это в свою очередь преобразование данных в вид, который признаёт алгоритм, и обычно это двумерный массив (матрица) значений, где каждая строка - пример, а значения строки - значения признаков.

В случае с квартетом Энскомба мы этого достигли преобразованием .reshape(-1, 1), где количество признаков это 1, а -1 - это количество примеров (мы могли подставить туда их точное количество, но для одной оси в reshape можно поставить и -1, тогда оно само подсчитается).

Препроцессинг этим не ограничивается. Что если мы хотим использовать категориальный признак? Например, пол ракушки? Алгоритмы ничего кроме чисел не понимают. Поэтомы мы должны привести их к числам, но не просто по порядку - порядок полов в данных же не важен, а векторизовать.

То есть мужскому полу сопоставить вектор (1, 0, 0), женскому (0, 1, 0), а детскому соответственно (0, 0, 1), и вместо одного признака для модели, у нас будет их три.

# всё это можно сделать функцией pandas get_dummies

processed_data = pd.get_dummies(dataframe['sex'])
processed_data.head()

	F	I	M
0	0	0	1
1	0	0	1
2	1	0	0
3	0	0	1
4	0	1	0

# чтобы две таблицы склеить по индексу, можно использовать такой код

number_data = processed_data.join(dataframe).drop('sex', axis='columns')
number_data.head()

	F	I	M	length	diameter	height	whole weight	shucked weight	viscera weight	shell weight	rings
0	0	0	1	0.455	0.365	0.095	0.5140	0.2245	0.1010	0.150	15
1	0	0	1	0.350	0.265	0.090	0.2255	0.0995	0.0485	0.070	7
2	1	0	0	0.530	0.420	0.135	0.6770	0.2565	0.1415	0.210	9
3	0	0	1	0.440	0.365	0.125	0.5160	0.2155	0.1140	0.155	10
4	0	1	0	0.330	0.255	0.080	0.2050	0.0895	0.0395	0.055	7

И теперь у нас готовые численные данные, которые можно отдавать в алгоритмы. А какие - об этом прямо сейчас.

2.3 Линейные модели и градиентный спуск¶

Линейные модели просты и интерпретируемы, и поэтому чрезвычайно распространены. И при подходящей предобработке признаков - весьма универсальны. Отклик по линейному алгоритму моделируется как линейная комбинация m признаков с некоторыми коэффициентами и плюс сдвиг:

\[y = \sum k_i x_i + b\]

Всё. Нет, не всё. Существует аналитическое решение (то есть формульно), как найти k1, ... km, b такие, чтобы ошибка (конкретно среднее квадратичное отклонение модели от данных) было минимальным. Мы же для целей иллюстрации рассмотрим алгоритм градиентного спуска, который применяется во множестве моделях, нейросетях в частности в различных модификациях.

Смысл всего этого такой. Чтобы найти минимум ошибки,

надо взять производную от этой самой ошибки по коэффициентам,
Далее двигаться в направлении уменьшения ошибки, изменяя случайно инициализированные коэффициенты на минус производную (то есть в сторону убывания ошибки),
И так сколько раз, сколько захотим (или пока ошибка не начнет меняться очень слабо).

Например, если у нас $y = kx + b$, а ошибка $$e = \frac {\sum (y - kx - b)^2} {n},$$ то производная ошибки по `k` будет равна $$e'_k = -2 \frac {\sum(x (y - kx - b))} {n},$$ а для `b`: $$e'_b = -2 \frac {\sum(kx - y - b)} {n}.$$

На деле же, существуют фреймворки (библиотеки), которые подобное дифференцирование делают за нас: tensorflow, pytorch. Их обычно используют для нейросетей. Но тут мы сделаем всё сами, чтобы убедиться, что всё это работает.

def update(x, y, k, b, alpha):
    number = len(y)
    
    # подсчитаем производные по коэффициентам
    change_k = -2 * sum([
        x[index] * (y[index] - k * x[index] - b) for index in range(number)
    ])
    change_b = -2 * sum([
        x[index] * k - y[index] - b for index in range(number)
    ])
    
    # параметр alpha - называется скорость обучения
    new_k = k - alpha * change_k / number 
    new_b = b - alpha * change_b / number 
    
    return new_k, new_b

def train_linear(x, y, alpha=0.1, epochs=50):
    # инициализируем случайно наши коэффициенты модели
    k, b = np.random.uniform(-1, 1), np.random.uniform(-1, 1)
    
    for epoch in range(epochs):
        k, b = update(x, y, k, b, alpha)
        
        if epoch % 10 == 0 and epoch > 0: # каждый десятый шаг
            print("%0d: среднее абсолютное отклонение численно составляет %.4f" % (
                epoch,
                np.mean(np.abs(y - k*x - b))
            ))
    
    return k, b

%%time

from sklearn.utils import shuffle

random_indices = shuffle(range(len(dataframe)), random_state=1)
train_indices = random_indices[:-300] # 300 точек - будет тест
test_indices = random_indices[-300:]

k, b = train_linear(
    dataframe['length'].values[train_indices],
    dataframe['diameter'].values[train_indices]
)

среднее абсолютное отклонение численно составляет 0.1942
среднее абсолютное отклонение численно составляет 0.0665
среднее абсолютное отклонение численно составляет 0.0137

40: среднее абсолютное отклонение численно составляет 0.0127
Wall time: 378 ms

plt.title('Результаты модели');
plt.scatter(dataframe['length'], dataframe['diameter']);
plt.plot(dataframe['length'], k * dataframe['length'] + b, c='orange');
plt.annotate("Запомним эту точку под\nназванием \"выброс\"", (0.185, 0.38), (0.2, 0.5), arrowprops={"arrowstyle": '->'});

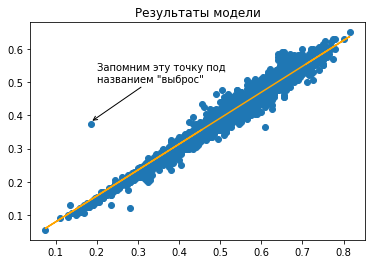
Congratulations!!

Паззлы сошлись, наша прямая подошла к данным. Замечательнейшая библиотека scikit-learn имеет множество вариаций линейных моделей в арсенале. И мы рассмотрим модели линейной регрессии и модель Ridge. Линейная модель - минимизирует средний квадрат отклонений предсказанного от истинного и может быть решена алгебраически (то есть без итераций, и работает поэтому быстро). Ridge (гребневая регрессия) отличается тем, что штрафует модель за абсолютную величину коэффициентов, это часто позволяет избегать переобучения.

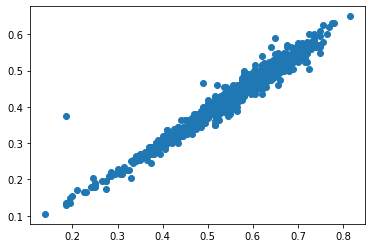
Учтите, что на линейные модели влияют выбросы в данных. Выбросы - это редкие точки, которые сильно отличаются от поведения всех остальных. Часто при препроцессинге их просто удаляют из датасета. Здесь “плотность” точек очень высокая, и влияние выбросов небольшое. Для иллюстрации, возьмем только вторую четверть датасета.

sliced = slice(len(train_indices) // 4, len(train_indices) // 2)
plt.scatter(dataframe['length'][sliced], dataframe['diameter'][sliced]);

from sklearn.linear_model import LinearRegression, Ridge

linear_model = LinearRegression().fit(
    dataframe.length.values[train_indices][sliced].reshape(-1, 1),
    dataframe.diameter[train_indices][sliced].values
)

ridge_model = Ridge(
    # это настройка штрафа, чем она выше, тем сильнее регуляризация
    alpha=1.25
).fit(
    dataframe.length.values[train_indices][sliced].reshape(-1, 1),
    dataframe.diameter[train_indices][sliced].values
)

k, b = train_linear(
    dataframe['length'].values[train_indices][sliced],
    dataframe['diameter'].values[train_indices][sliced]
)

# а предскажем - на тестовом
linear_predictions = linear_model.predict(
    dataframe.length.values[test_indices].reshape(-1, 1)
)

ridge_predictions = ridge_model.predict(
    dataframe.length.values[test_indices].reshape(-1, 1)
)

plt.title('Результаты моделей на тестовом множестве');
plt.scatter(dataframe['length'].values[test_indices], dataframe['diameter'].values[test_indices], alpha=0.1);
plt.plot(dataframe['length'].values[test_indices], k * dataframe['length'].values[test_indices] + b, ls='--', c='orange', label="Наивная");
plt.plot(dataframe['length'].values[test_indices], linear_predictions, c='green', ls='--', label="Linear");
plt.plot(dataframe['length'].values[test_indices], ridge_predictions, c='red', ls='--', label="Ridge");
plt.legend(loc='best');

среднее абсолютное отклонение численно составляет 0.1575
среднее абсолютное отклонение численно составляет 0.0137
среднее абсолютное отклонение численно составляет 0.0177
среднее абсолютное отклонение численно составляет 0.0134

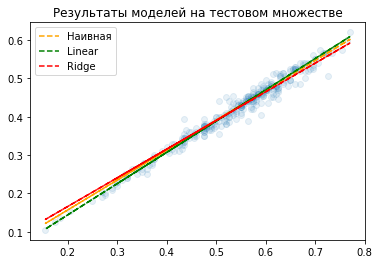
Как видим, наша модель отличается. Давайте проверим метрику R-квадрат на отложенном тесте. Это самая распространенная метрика для задачи регрессии. Она всегда меньше либо равна единице, чем ближе к единице - тем лучше предсказания модели совпадают с истинными значениями. Если она равна нулю, то предсказание идёт средним значением целевой величины (ниже нуля - еще хуже).

from sklearn.metrics import r2_score

print("Наивная модель на тестовом множестве %.5f, Linear и Ridge (там же): %.5f, %.5f" % (
    r2_score(dataframe.diameter.values[test_indices], k * dataframe['length'].values[test_indices] + b),
    r2_score(dataframe.diameter.values[test_indices], linear_predictions),
    r2_score(dataframe.diameter.values[test_indices], ridge_predictions)
))

Наивная модель на тестовом множестве 0.97413, Linear и Ridge (там же): 0.97425, 0.97177

Как видим, качество отличается в третьем знаке после запятой. Нам тут сильно повезло с данными… :) А давайте посмотрим, как можно решить задачу классификации с помощью линейной модели.

Наша модель будет иметь вид

\[y = \sigma (\sum k_i x_i + b)\]

где $\sigma$ (sigmoid), это следующая функция

\[\sigma(x) = \frac {1} {1 + e^{-x}}.\]

Она всегда от 0 до 1 невключительно. Её можно интерпретировать как вероятность того, что пример с признаками x1, ..., xm относится к классу 1 (а не 0). В scikit-learn модель заведена под названием LogisticRegression (это не регрессия, несмотря на название, а классификация).

Попробуем отличить применить логистическую регрессию к датасету Iris.

from sklearn.linear_model import LogisticRegression

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

X, y = load_iris(return_X_y=True)

# оставим только два последних признака
X = X[:, -2:]

X_train, X_test, y_train, y_test = train_test_split(
    X, y,
    test_size=0.2, random_state=1, shuffle=True
)

# создадим модель
logreg = LogisticRegression(random_state=1, multi_class='auto').fit(X_train, y_train)

from sklearn.metrics import accuracy_score # метрика - количество правильных ответов

print("Точность классификации на %d тестовых примерах %.3f" % (
    len(y_test),
    accuracy_score(
        y_test,
        logreg.predict(X_test)
    )
))

Точность классификации на 30 тестовых примерах 0.967

from sklearn.metrics import confusion_matrix 
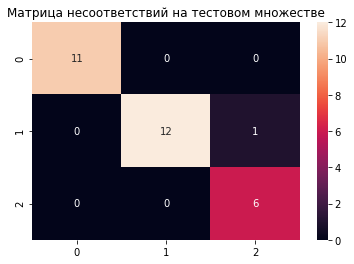
plt.title("Матрица несоответствий на тестовом множестве")
sns.heatmap(confusion_matrix(
    y_test,
    logreg.predict(X_test)
), annot=True);

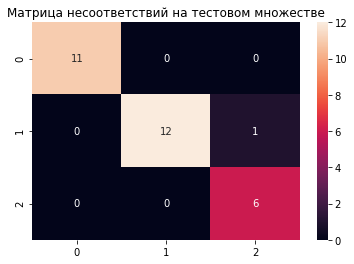
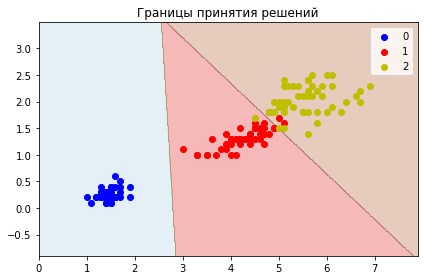
Как видим, здесь хороший случай, практически линейно разделимый. Посмотрим, как разделились классы на плоскости.

def plot_decisions(x, y, targets, classifier, labels=None):
    x_min, x_max = x.min() - 1, x.max() + 1
    y_min, y_max = y.min() - 1, y.max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01),
                         np.arange(y_min, y_max, 0.01))

    z = classifier.predict(np.c_[xx.ravel(), yy.ravel()])
    z = z.reshape(xx.shape)
    c = plt.contourf(xx, yy, z, cmap='Paired', alpha=0.3)
    
    for index in range(len(pd.unique(targets))):
        indices = np.where(targets == index)
        plt.scatter(x[indices], y[indices], color=[
            'b', 'r', 'y'
        ][index], label=labels[index] if labels is not None else index)

    plt.legend()
    plt.tight_layout()
    plt.show()

plt.title('Границы принятия решений');
plot_decisions(
    X[:, 0],
    X[:, 1],
    y,
    logreg
)

Небольшое заключение¶

Линейные модели далеко не всегда без подходящего feature engineering хорошо работают. А практически - никогда (без изменения признаков). В моделируемых процессах часто очень мало линейного. Далее у нас будет кое-что помощнее!

2.4 Деревья решений и ансамбли моделей на их основе¶

Дерево решений - это алгоритм, который строит модели такого вида:

Tree

При этом дерево может быть любой глубины, но в конечных его узлах (листах) - всегда стоят конкретные значения целевой величины (числа для регрессии или классы).

Но тут, конечно же, вопрос - откуда берутся промежуточные значения, с которыми сравниваются признаки?

Они выбираются так, чтобы при разбиении на две части, уменьшалась энтропия по целевым меткам - это величина, которая тем ближе к единице, чем равномерно случайнее разбросаны в итоге метки, и тем ближе к нулю, чем все метки ближе к единому значению.

То есть если метки разбиты как 50/50 - энтропия 1, если как 0/100 (есть только одна метка) - энтропия 0.

Давайте посмотрим как работает одиночное дерево на наших ракушках.

from sklearn.tree import DecisionTreeClassifier, plot_tree

# деревья by design умеют в мультикласс
decision_tree = DecisionTreeClassifier(random_state=1).fit(X_train, y_train).fit(X_train, y_train)

plt.title("Матрица несоответствий на тестовом множестве")
sns.heatmap(confusion_matrix(y_test, decision_tree.predict(X_test)), annot=True);

plt.title('Как дерево подобрало пороги');
plot_decisions(
    X[:,0],
    X[:,1],
    y,
    decision_tree
)

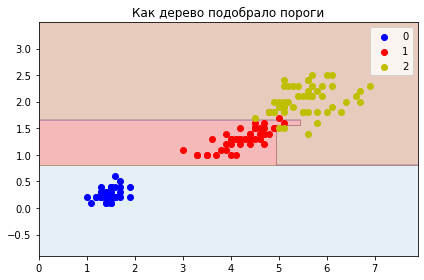
Здесь мы не стали ограничивать дерево по глубине, и видно, что оно “слишком глубоко” погрузилось в данные.

Одиночные деревья - всегда переобучаются!

Для иллюстрации - обрежем по глубине.

decision_tree_shallow = DecisionTreeClassifier(
    criterion='entropy',
    max_depth=3, # максимум 3 вопроса
    random_state=1
).fit(X_train, y_train)

plt.title('Другая граница решений')
plot_decisions(
    X[:,0],
    X[:,1],
    y,
    decision_tree_shallow
)

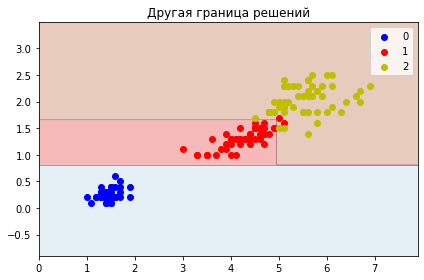
plt.figure(figsize=(10, 10))
plot_tree(decision_tree_shallow, filled=True);

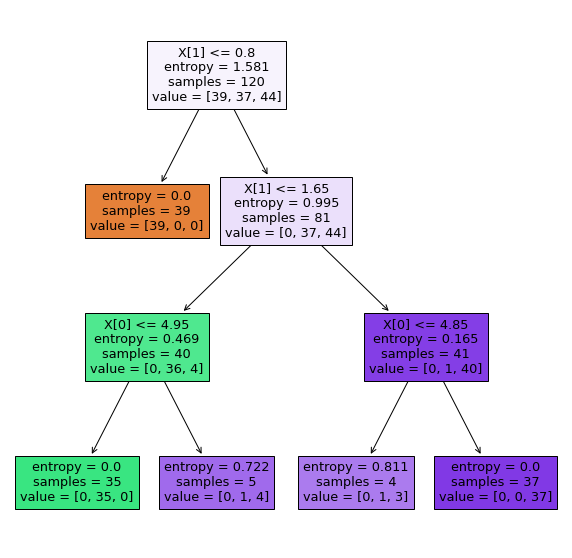
Одиночные деревья - очень интерпретируемые модели, но они редко когда сами по себе полезны. Полезны ансамбли деревьев. Рассмотрим два:

Случайный лес решающих деревьев.

Это множество решающих деревьев, когда каждое дерево обычно строится в полную глубину, но не на всех признаках и не на всех примерах, а на их случайных подмножествах. Ответы полученных деревьев усредняются.

Градиентный бустинг над решающими деревьями.

Это множество чаще всего неглубоких решающих деревьев, применяемых последовательно, каждое следующее дерево - исправляет ошибки предыдущего.

Как ни удивительно, эти методы очень хорошо работают.

ВАЖНО! Для задач регрессии, по построению деревья не могут выходить за пределы тех предсказываемых значений, которые видели деревья на обучающем множестве!

Это означает, что если вам надо экстраполировать (величина может выходить за пределы обучающих примеров), деревья не подойдут!

from sklearn.ensemble import GradientBoostingClassifier, RandomForestClassifier

boosting = GradientBoostingClassifier(
    n_estimators=10, # количество деревьев
    max_depth=5, # глубина деревьев
    random_state=1
).fit(X_train, y_train)

forest = RandomForestClassifier(
    n_estimators=10,
    random_state=1
).fit(X_train, y_train)

plt.title("Матрица несоответствий на тестовом множестве для градиентного бустинга")
sns.heatmap(confusion_matrix(y_test, boosting.predict(X_test)), annot=True);

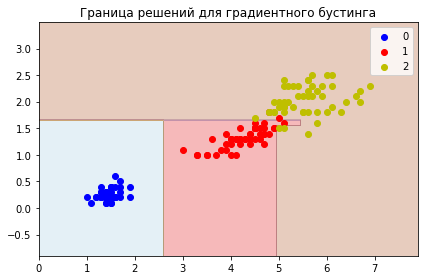
plt.title('Граница решений для градиентного бустинга')
plot_decisions(
    X[:,0],
    X[:,1],
    y,
    boosting
)

plt.title("Матрица несоответствий на тестовом множестве для случайного леса")
sns.heatmap(confusion_matrix(y_test, forest.predict(X_test)), annot=True);

plt.title('Граница решений для случайного леса')
plot_decisions(
    X[:,0],
    X[:,1],
    y,
    forest
)

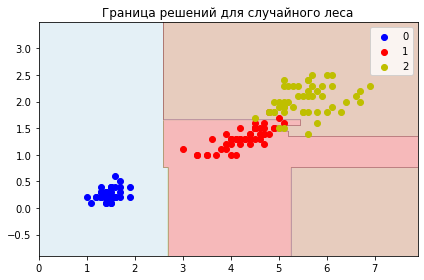
Как видим, ансамбли работают отлично от одиночного дерева, и от линейных алгоритмов, несмотря на то, что ошибаются одинаково (в одном цветке).

Заключение¶

Ансамбли на основе деревьев могут разбирать очень сложные данные. Они часто применяются на практике и дают хорошие результаты. Но никакие деревья не справятся с ситуацией, когда данные слишком запутанные или схожие, или нет золотого признака, то есть такого признака, по которому хорошо различается целевая величина.

Если RandomForest или GradientBoosting для данных - подходящий алгоритм в случае регрессии, то можно так же из них получать прогнозные интервалы. Для первого можно обойти все деревья ансамбля (rf.estimators_), для каждой точки сделать предсказания каждым деревом и выбрать процентиль (np.percentile). Для градиентного бустинга схема немного другая: там нужно использовать параметры loss = 'quantile' и alpha = 0.5, где alpha - можно регулирует границу интервала от 0 до 1, 0.5 соответствует среднему предсказанию (тому, который обычно отдает бустинг).

2.5 Алгоритм ближайших соседей (и немного о текстах)¶

Мы уже пользовались им на предыдущей лекции. Ближайшие соседи - это, получается, такая база данных, которая запоминает правильные ответы, а потом использует ближайшие похожие случаи для предсказания.

Начнем сразу с интерактивного примера на датасете Iris.

from sklearn.neighbors import KNeighborsClassifier

# обучим на всём датасете
knn_classifier = KNeighborsClassifier(n_neighbors=3).fit(X, y)

def plot_point(point_x, point_y):
    sort = knn_classifier.predict([[point_x, point_y]])[0]
    
    plt.title("Предсказанный класс %d" % sort);
    plt.scatter(
        X[:, 0].tolist() + [point_x],
        X[:, 1].tolist() + [point_y],
        c=y.tolist() + [sort]
    );
    plt.annotate(
        "Наша точка",
        (point_x, point_y),
        (point_x + 0.25, point_y + 0.25),
        arrowprops={"arrowstyle": '->'}
    );
    
interact(
    plot_point, 
    point_x=(0, 7.5, 0.2),
    point_y=(0, 3.5, 0.2)
);

plt.title('Граница решений для ближайших соседей')
plot_decisions(
    X[:,0],
    X[:,1],
    y,
    KNeighborsClassifier(n_neighbors=3).fit(X_train, y_train)
)

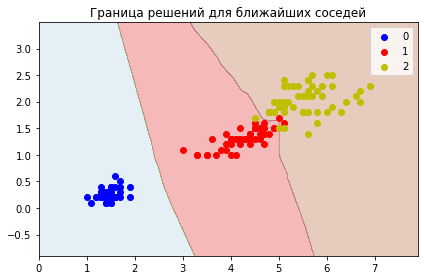
Как оказалось, даже такие простые данные имеют локальные запутанности!

А зачем вообще нужны ближайшие соседи, если они всё запоминают? На самом деле чаще всего важно найти именно одного ближайшего соседа. Давайте рассмотрим пример.

Пусть у нас есть набор текстовых обращений в техническую поддержку какого-нибудь провайдера (например из чата на сайте).

Провайдер предоставляет услуги ТВ и интернета. Он хотел бы знать, поступившее обращение - оно про ТВ или про Интернет? Чтобы автоматически отправлять его в подходящую группу специалистов.

texts = [
    "Не работает интернет!", "Не работает телевидение", "Проблемы с телевидением", "Интернет сломался"
]

# Импортируем один из самых простых "векторизаторов" текстов
# он укладывает вектора на единичную сферу

from sklearn.feature_extraction.text import HashingVectorizer
vectorizer = HashingVectorizer(n_features=3).fit(texts)
space = vectorizer.transform(texts)

print("Вектора текстов")
print(space.todense())

Вектора текстов
[[ 0.4472136   0.          0.89442719]
 [ 0.4472136   0.          0.89442719]
 [-0.70710678  0.70710678  0.        ]
 [ 0.70710678  0.          0.70710678]]

from sklearn.neighbors import NearestNeighbors

# инстанцируем объект, который будет находить ближайшего соседа
nearest = NearestNeighbors(n_neighbors=1).fit(space)

text = "Что-то не так с интернетом"
index = nearest.kneighbors(vectorizer.transform([text]), return_distance=False)[0][0]
print("Ближайший сосед %s: " % text, texts[index])

text = "Что за ерунда с ТВ!"
index = nearest.kneighbors(vectorizer.transform([text]), return_distance=False)[0][0]
print("Ближайший сосед %s: " % text, texts[index])

Ближайший сосед Что-то не так с интернетом:  Не работает интернет!
Ближайший сосед Что за ерунда с ТВ!:  Проблемы с телевидением

В данном случае это очень ограниченный пример, который может (и будет) давать ошибки. Он ничего на самом деле не понимает в языке. Но главное в нём - идея ближайших. Далее в лекциях мы увидим и узнаем как использовать гораздо более лучшие языковые модели. Уже готовые.

Но основная идея их использования будет та же.

На практике же часто работают с двумя векторизаторами текстов: CountVectorizer и TfIdfVectorizer. И первый и второй относятся к текстам как к “мешку слов” - то есть не учитывают порядок слов в тексте, а просто работают с наличием. Первый - подсчитывает количество вхождений слов в текст, второй подсчитывает не просто количество вхождений слова в документ, но и делает поправку на то, как часто оно встречается в других документах (term-frequency inverse-document-frequency). Это нужно для того, чтобы более редкие слова имели вес больше, чем часто встречающиеся в наборе.

Давайте рассмотрим датасет 20 newsgroups - различные посты по 20 темам, всего их около 18 тысяч.

from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer

# загрузим без заголовков, они содержат email автора и прочие отделимые вещи
data_train = fetch_20newsgroups(subset='train', random_state=1, remove=('headers'))
data_test = fetch_20newsgroups(subset='test', random_state=1, remove=('headers'))

data_train.data[0][:100], data_train.target_names[data_train.target[0]]

("Well i'm not sure about the story nad it did seem biased. What\nI disagree with is your statement tha",
 'talk.politics.mideast')

Поскольку в каждом тексте есть предлоги, союзы и прочие часто встречающиеся стоп-слова, мы просто удалим их из текста, чтобы не мешались (они не очень влияют на “смысл” мешка слов).

from stop_words import get_stop_words
stop_words = get_stop_words('en') # здесь может быть 'ru'
stop_words[0], len(stop_words)

('a', 174)

Далее, для каждого слова - найдем его основу (“приветики - приветик”). Это называется стемминг (stemming), и это не то же самое, что нахождение корня слова (хотя изредка может совпадать). Для английского и некоторых языков, включая русский, такой функционал есть в библиотеке nltk. Стемминг - это детерминированный алгоритм, который работает с гласными/согласными буквами, слогами, по некоторым сложным правилам. Стемминг вообще нам нужен для того, чтобы не различать форму слова.

# векторизуем наши сперва почищенные тексты

from nltk.stem.snowball import SnowballStemmer
stemmer = SnowballStemmer("english")

def clear_words(text):
    result = []
    for word in text.lower().split():
        stripped = word.strip()
        if stripped in stop_words:
            continue
        result.append(stemmer.stem(stripped))
    return ' '.join(result)

texts_train, texts_test = [
    clear_words(text) for text in data_train.data
], [
    clear_words(text) for text in data_test.data
]

tfidf = TfidfVectorizer(
    # слово должно встречаться хотя бы в 1% документов
    min_df=0.01,
    # слово не должно быть в каждом пятом документе!
    max_df=0.20
).fit(texts_train)

vectors_train = tfidf.transform(texts_train)
vectors_test = tfidf.transform(texts_test)

vectors_train.shape, vectors_test.shape

Что это за размерность такая, можно спросить? Первая понятно, документы, а второе - это все слова, которые попадаются в документах. Но поскольку они не так часто все во всех встречаются, полученные матрицы - разреженные.

np.random.seed(1)
print("Десять случайных слов %s" % str(
    np.array(tfidf.get_feature_names())[np.random.randint(0, len(tfidf.get_feature_names()), size=10)].tolist()
))

Десять случайных слов ['meant', 'aw', 'mix', 'was', 'intend', 'fli', 'then', 'howev', 'known', 'allow']

from sklearn.neighbors import KNeighborsClassifier

text_classifier = KNeighborsClassifier(100, metric='cosine').fit(
    vectors_train.todense(), data_train.target
)

data_test.target_names[text_classifier.predict(
    vectors_test.todense()[0].reshape(1, -1)
)[0]], \
data_test.target_names[data_test.target[0]]

('rec.sport.baseball', 'rec.sport.baseball')

"Accuracy %.3f" % text_classifier.score(vectors_test.todense(), data_test.target)

'Accuracy 0.622'

Здесь для сравнения использутся метрика косинусного сходства, она сравнивает угол между векторами (от разнонаправленных: -1 до сонаправленных: +1). Это означает что влияет не столько длина вектора примера (кстати после tf idf они все нормированы к единичной евклидовой длине), сколько именно направление.

Почему влияет именно направление? Потому что у нас оси - это конкретные слова, и наличие чего-то отличного от нуля в этом направлении уже говорит о некоторой смысловой нагрузке в тексте. Например, слово “политический” сильно отличается “мяч”, и представьте, у нас только две таких оси. В этом случае, чем ближе текст по направлению к таким же с “мячом”, тем скорее он про спорт, нежели про политику. Пример текста про посещение политиками футбольного матча - будет где-то под 45 градусов в наших осях :)

Немного заключения¶

Поиск ближайших - очень распространенный метод работы с данными. Существуют эффективные библиотеки для работы с такими данными, например faiss или annoy. Если данные группируются каким-то образом, то ближайшие соседи - быстрый и рабочий способ.

2.6 Нейросети в `scikit-learn`¶

Кульминация, так сказать, сегодняшнего дня. Рассмотрим как можно строить регрессоры и классификаторы с помощью нейронных сетей.

Что такое нейронная сеть? Это набор слоёв, на каждом слое - несколько нейронов, каждый из которых это линейная модель, к которой применили функцию активации. Нейроны в полносвязной сети на каждом слое связаны со всеми нейронами следующего слоя.

Функция активации - это нелинейная функция, чаще всего это $relu(x) = max(0, x)$ или $tanh(x) = \frac {e^{2x} - 1} {e^{2x} + 1}$.

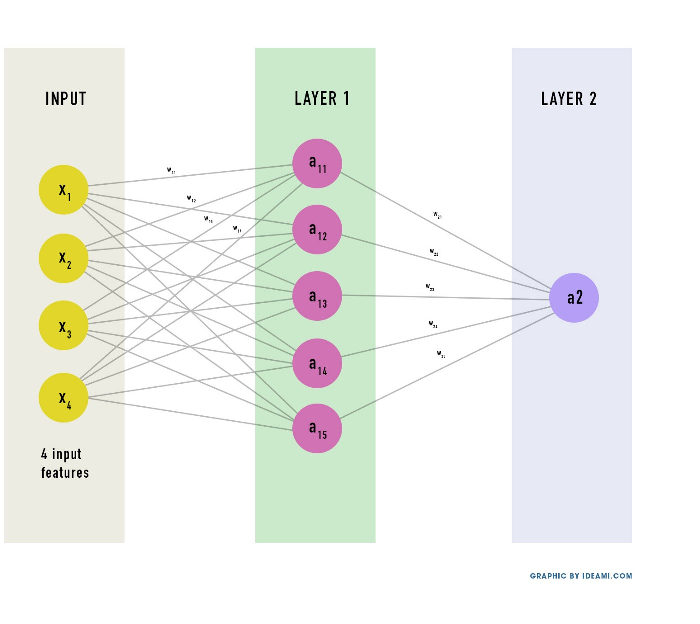
Dense NN

В простейшем случае, с одним слоем, одним нейроном и relu-активацией, нейросеть представляет собой функцию $y = max(0, \sum x_i k_i + b)$. В более сложном случае, такое выражение - это каждый нейрон сети. И каждый нейрон по сети “глубже” - зависит от вычислений на предыдущих нейронах.

Чем хороши нейронные сети? Тем что они являются универсальным аппроксиматором - то есть ими - при подходящих условиях (например когда нейронов достаточное число) можно приближать функции (есть теорема Цыбенко, о том что полносвязной сетью с одним скрытым слоем и сигмоидной активацией можно аппроксимировать любую непрерывную функцию многих переменных с любой точностью).

Кристофер Олах - сотрудник OpenAI (Илона Маска) - сделал даже вот такую анимацию, как сети поступают с данными. Здесь нейросеть итеративно подбирает веса таким образом, чтобы две спиральных линии после преобразований нейросетью стали линейно разделимыми.

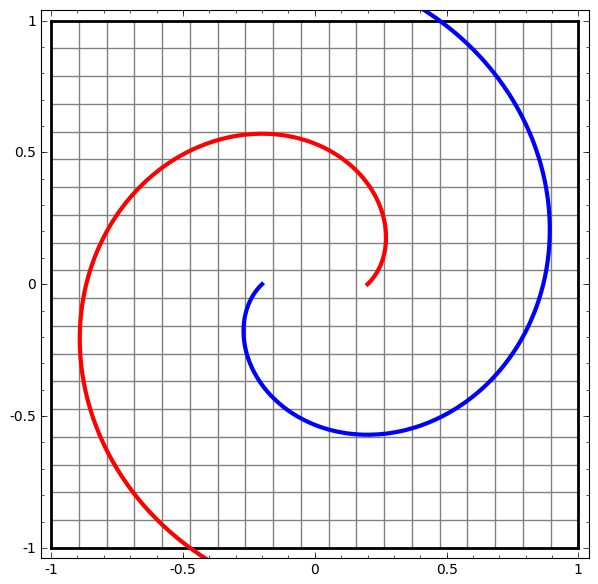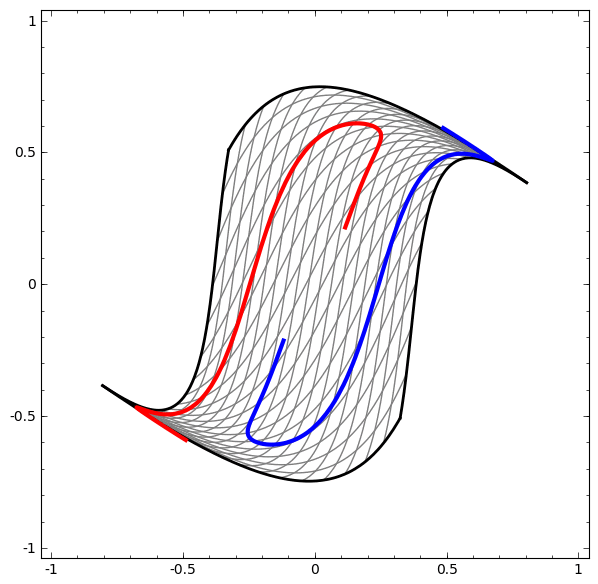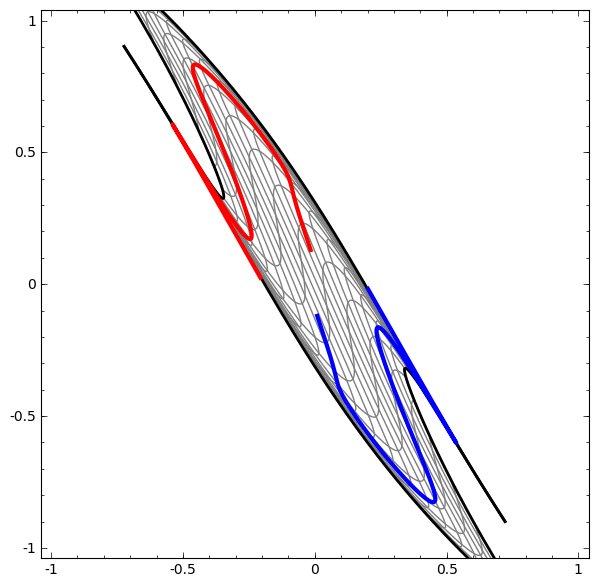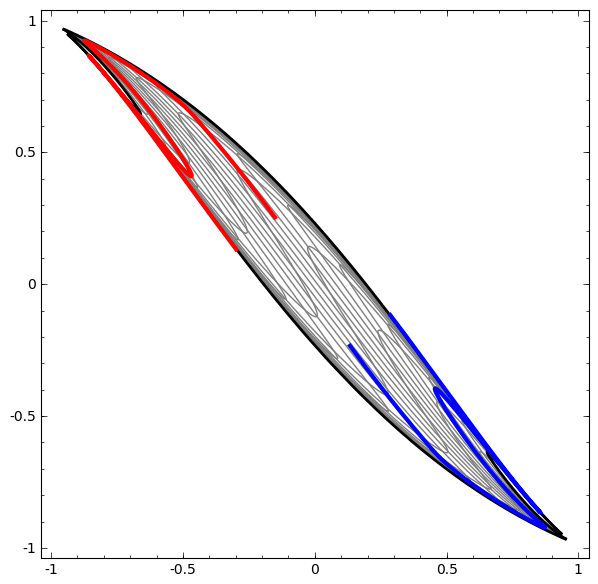
Olahs

Именно поэтому и говорят, что нейросети умеют сами в feature engineering (то есть вместо ручных преобразований данных до линейной разделимости, это делает сеть). На самом деле, хорошо в него умеют именно глубокие сети (deep neural networks), это когда слоев много, и они не просто “всё связано со всем”, а имеют в себе некоторую логику для получения весов. Неглубоким (shallow) сетям, feature engineering не помешает.

ОДНАКО. Если мы используем функции активации, то мы должны для нейросетей использовать подходящий препроцессинг. Например, поскольку tanh меняется от -1 до 1, то и наша целевая величина должна меняться в тех же пределах! Это не совсем так уже для relu (его результат всегда больше нуля), но дело еще и в другом.

Нейросети хорошо работают с маленькими числами, так как большие числа дают большие значения производных. Соответственно тогда легко проскочить минимум функции ошибки, при движении большими шагами.

Поэтому мы рассмотрим два способа подготовки данных для нейросети: standard scaling и minmax scaling.

# вернемся к датасету ракушек

data = pd.read_csv('data/abalone.csv')
data = pd.get_dummies(data.sex).join(data).drop(['sex'], axis='columns')

features = list(data.columns)
features.remove('rings')

'Наши признаки', features

('Наши признаки',
 ['F',
  'I',
  'M',
  'length',
  'diameter',
  'height',
  'whole weight',
  'shucked weight',
  'viscera weight',
  'shell weight'])

Начнем с задачи предсказания количества колец.

# качество будем оценивать по кросс-валидации
from sklearn.model_selection import cross_val_score

from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.neural_network import MLPRegressor, MLPClassifier

# standard scaler - вычитает среднее и делит на разброс
changed = list(features)
for change in ['F', 'M', 'I']:
    changed.remove(change)

# при преобразовании пропустим признаки пола    
shuffled_X, shuffled_y = shuffle(
    np.hstack([
        data[['F', 'M', 'I']].values.reshape(-1, 3),
        StandardScaler().fit_transform(data[changed])
    ]),
    data['rings'].values + 1.5, # перейдем сразу к возрасту
    random_state=1
)

target_scaler = StandardScaler()
scaled_target = target_scaler.fit_transform(shuffled_y.reshape(-1, 1))

regressor = MLPRegressor(
    hidden_layer_sizes=[20, 20], # два скрытых слоя на 20 нейронов
    activation='relu',
    max_iter=1000, # сколько итераций подгонки
    random_state=1 # для воспроизводимости
)

scores = cross_val_score(
    regressor,
    X=shuffled_X,
    y=scaled_target.flatten(), # сделаем массив "плоским"
    cv=3,
    scoring='r2'
)

"R2 mean: %.3f, std %.3f" % (scores.mean(), scores.std())

'R2 mean: 0.521, std 0.070'

Не очень-то большой R2. В чем дело? Если вспомнить наши попарные диаграммы, то там можно было увидеть выбросы. Давайте почистим данные от них.

sns.pairplot(data=pd.read_csv('data/abalone.csv')[['height', 'diameter', 'sex']], hue='sex');

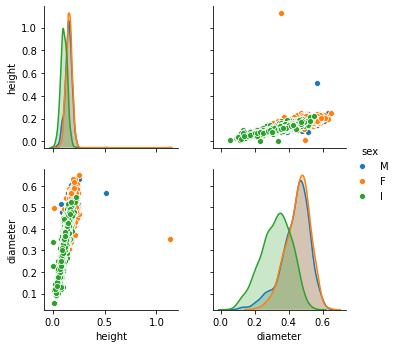
bad_indices = shuffle(np.where(data.height > 0.4), random_state=1)[0]
good_indices = list(range(len(data)))

for index in bad_indices: good_indices.remove(index)

bad_indices

array([1417, 2051], dtype=int64)

Выкинем их из данных и попробуем еще раз!

regressor = MLPRegressor(
    hidden_layer_sizes=[20, 20], # два скрытых слоя на 20 нейронов
    activation='relu',
    max_iter=1000, # сколько итераций подгонки
    random_state=1 # для воспроизводимости
)

scores = cross_val_score(
    regressor,
    X=shuffled_X[good_indices],
    y=scaled_target.flatten()[good_indices], # сделаем массив "плоским"
    cv=3,
    scoring='r2'
)

"R2 mean: %.3f, std %.3f" % (scores.mean(), scores.std())

'R2 mean: 0.572, std 0.016'

Метрика улучшилась! Но пока еще недостаточно.

shuffled_X = shuffled_X[good_indices]
shuffled_y = shuffled_y[good_indices]

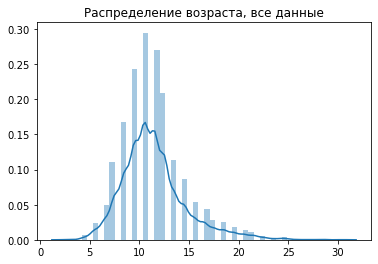
plt.title('Распределение возраста, все данные');
sns.distplot(shuffled_y);

train = int(len(shuffled_y) * 0.8)
test = len(shuffled_y) - train

from sklearn.preprocessing import PowerTransformer
target_processor = PowerTransformer().fit(shuffled_y[:train].reshape(-1, 1))
transformed_y = target_processor.transform(shuffled_y.reshape(-1, 1)).flatten()

plt.title('Трансформированная целевая величина train/test')
sns.distplot(transformed_y[:train]);
sns.distplot(transformed_y[train:]);

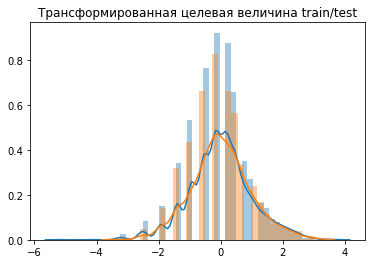
Что такое PowerTransform? Помните как мы подбирали третью степень для длины и веса? PowerTransform подбирает для одной величины степенное преобразование так, чтобы её распределение было как можно более близко к нормальному.

from sklearn.metrics import mean_absolute_error

regressor = MLPRegressor(
    hidden_layer_sizes=[20, 20], 
    activation='relu',
    max_iter=1000, 
    random_state=1 
)

regressor.fit(
    shuffled_X[:train],
    transformed_y[:train]
)

"R2 %.3f, ошибка в возрасте: %.2f, разброс значений возраста %.2f" % (
    r2_score(
        shuffled_y[train:],
        target_processor.inverse_transform(
            regressor.predict(shuffled_X[train:]).reshape(-1, 1)
        )
    ),
    mean_absolute_error(
        shuffled_y[train:],
        target_processor.inverse_transform(
            regressor.predict(shuffled_X[train:]).reshape(-1, 1)
        )
    ),
    shuffled_y[train:].std()
)

'R2 0.597, ошибка в возрасте: 1.43, разброс значений возраста 3.12'

Посмотрим теперь классификацию на датасете Iris.

classifier = MLPClassifier(
    hidden_layer_sizes=[32, 12],
    activation='tanh',
    max_iter=1000,
    random_state=1
)

X_changed = MinMaxScaler(
    feature_range=(-1, 1)
).fit_transform(X)

scores = cross_val_score(
    classifier,
    X=X_changed,
    y=y,
    cv=3,
    scoring='accuracy'
)

"Accuracy mean: %.3f, std %.3f" % (scores.mean(), scores.std())

'Accuracy mean: 0.953, std 0.019'

iris_X, iris_y = shuffle(X_changed, y, random_state=1)
classifier.fit(iris_X[:-50], iris_y[:-50])

plt.title("Обратите внимание - оси отмасштабированы!")
plot_decisions(X_changed[:, 0], X_changed[:, 1], y, classifier)

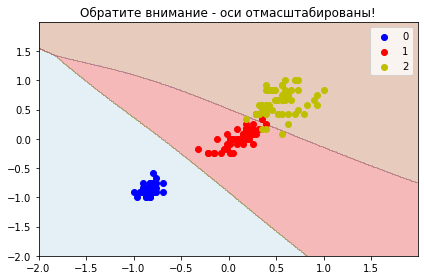
Здесь мы видим, как нейросетью можно разграничить классы датасета Iris.

Небольшое заключение¶

Несмотря на то, что сети универсальны, при добавлении одного признака, они требуют в квадрат больше примеров - ввиду своей как раз универсальности. Для табличных данных все же очень хорошо работают и другие алгоритмы в сочетании с feature engineering. Его же никто не запрещает использовать и для нейросетей.

ML introduction

День второй - анализ данных¶

2.1 Библиотеки работы с данными¶

Библиотеки numpy и pandas¶

Библиотеки визуализации¶

А теперь - интерактив!¶

2.2 Разведочный анализ и препроцессинг¶

2.3 Линейные модели и градиентный спуск¶

Небольшое заключение¶

2.4 Деревья решений и ансамбли моделей на их основе¶

Заключение¶

2.5 Алгоритм ближайших соседей (и немного о текстах)¶

Немного заключения¶

2.6 Нейросети в scikit-learn¶

Небольшое заключение¶

2.6 Нейросети в `scikit-learn`¶