Визуально о математике, стоящей за некоторыми алгоритмами¶
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
1. Градиентный спуск¶
Во многих алгоритмах градиентный спуск может применяться для оптимизации. Мы рассмотрим, что происходит при минимизации ошибки градиентных спуском.
from sklearn.datasets import make_regression
X, y = make_regression(n_samples=100, n_features=1, noise=10, random_state=1)
X = X.flatten()
plt.title('Синтетические данные')
plt.scatter(X, y);
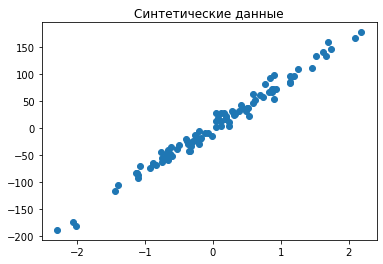
Воспользуемся кодом из второго дня, и немного его модифицируем для сохранения истории.
def update(x, y, k, b, alpha):
number = len(y)
change_k = -2 * sum([
x[index] * (y[index] - k * x[index] - b) for index in range(number)
])
change_b = -2 * sum([
x[index] * k - y[index] - b for index in range(number)
])
new_k = k - alpha * change_k / number
new_b = b - alpha * change_b / number
return new_k, new_b
def train_linear(x, y, alpha=0.1, epochs=50):
k, b = np.random.uniform(-1, 1), np.random.uniform(-1, 1)
history = []
for epoch in range(epochs):
k, b = update(x, y, k, b, alpha)
error = np.mean(np.abs(y - k*x - b))
history.append((k, b, error))
return k, b, history
Сперва посмотрим как с ростом количества эпох наша прямая всё ближе подходит к данным.
plt.subplots(5, figsize=(5, 20))
space = np.linspace(X.min(), X.max())
for index in range(0, 21, 5):
k, b, _ = train_linear(X, y, epochs=index - 1)
plt.subplot(5, 1, index // 5 + 1)
plt.title("Total epochs %d" % index)
plt.scatter(X, y);
plt.plot(space, space * k + b, c='red');
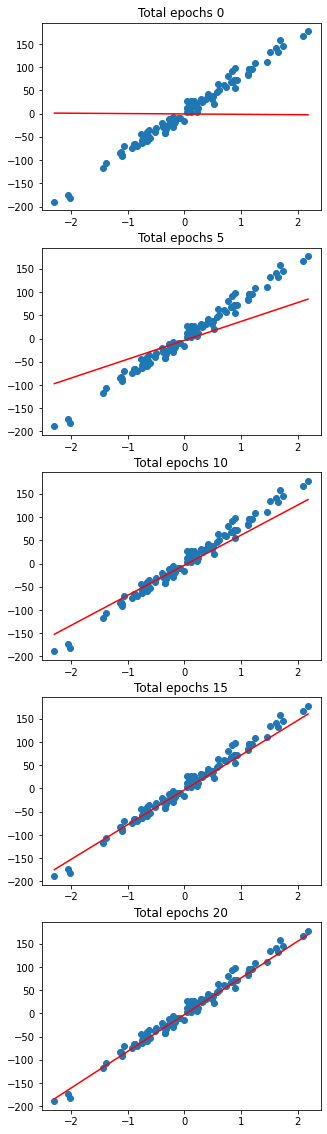
Посмотрим на “траекторию” градиентного спуска, где по осям - наши два коэффициента линейной модели, а по вертикали - ошибка.
from mpl_toolkits.mplot3d import Axes3D
axes = plt.subplot(projection='3d')
_, _, history = train_linear(X, y)
history = np.asarray(history).reshape(-1, 3)
plotted = axes.scatter(
history[:, 0],
history[:, 1],
history[:, 2],
c=np.arange(len(history)),
cmap='winter'
);
plt.colorbar(plotted);
axes.set_xlabel('k');
axes.set_ylabel('b');
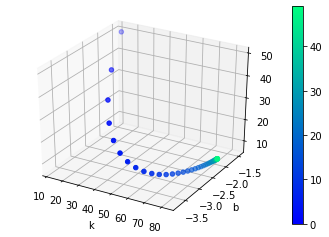
Наконец, отобразим тот же путь на поверхности ошибки - которая соответствует множеству пар k и b.
meshgrid = {"x": [], "y": [], "z": []}
for k in np.linspace(-50, 150, 100):
for b in np.linspace(-50, 50, 100):
meshgrid['x'] += [k]
meshgrid['y'] += [b]
meshgrid['z'] += [np.mean(np.abs(y - k*X - b))]
axes = plt.subplot(projection='3d')
axes.view_init(azim=70, elev=70)
plotted = axes.scatter(
meshgrid['x'],
meshgrid['y'],
meshgrid['z'],
c=meshgrid['z'],
cmap='Blues_r',
alpha=0.075
);
axes.scatter(
history[:, 0],
history[:, 1],
history[:, 2],
c=np.arange(len(history)),
cmap='winter',
s=50
);
axes.set_xlabel('k');
axes.set_ylabel('b');
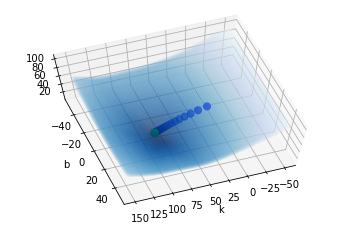
На рассмотренных отрезках k и b - у нас один оптимум, и он есть искомый минимум. Градиентным спуском алгоритм как раз к нему и приближается (сначала быстро, потом медленнее).
Практически аналогичным образом поступают оптимизаторы (rmsprop, adam) по весам нейронных сетей - только там параметров не два, а тысячи и миллионы, локальных оптимумов (глобальный всегда один) может быть не один - а большое множество, и те кривые метрик которые мы видим при обучении нейросети - это как раз один из вариантов отображения “пути” градиентного спуска.
Оптимизаторы отличаются тем, как они меняют шаг, как они “ускоряются в протяженных оврагах” и другими деталями, которые позволяют обучать сети эффективнее. Тем не менее в целом принцип - тот же.
2. Вычисления на графах¶
Вопрос, откуда берется производная ошибки по весам для нейросетей? Она вычисляется с помощью графа вычислений.
В основе лежит формула дифференцирования сложной функции: $\(f'(g(x)) = f'(u) = f'(u) \cdot u'(x)\)$
Теперь представим граф вычислений для функции f(x, y) = x + x * y.
В таком случае, в каждом узле надо взять производную и подсчитать (перемножением по формуле выше) саму производную. Например.
Пусть $\(a(x,y) = x \cdot y, b(x, y) = x, f(x, y) = a(x, y) + b(x, y)\)$
Тогда для получения частной производной по x:
$\(\frac {\partial f} {\partial x} = \frac {\partial f} {\partial a} \cdot \frac {\partial a} {\partial x} + \frac {\partial f} {\partial b} \cdot \frac {\partial b} {\partial x} = 1 \cdot y + 1 = y + 1\)$
Аналогично считается и производная по y:
$\(\frac {\partial f} {\partial y} = \frac {\partial f} {\partial a} \cdot \frac {\partial a} {\partial y} + \frac {\partial f} {\partial b} \cdot \frac {\partial b} {\partial y} = 1 \cdot x + 0 = x\)$
После получения градиентов можно уже использовать градиентный спуск.
Рассмотрим пример на tensorflow. В качестве данных выберем несложную однопараметрическую функцию.
def function(x, y, k=1):
return x**2 + y**2 + k**2
space = np.linspace(-1, 1, 200)
data = np.array([
[
x, y, function(x, y)
] for x in space for y in space
]).reshape(-1, 3)
axes = plt.subplot(projection='3d')
plotted = axes.scatter(
data[:, 0],
data[:, 1],
data[:, 2],
c=data[:, 2],
cmap='Blues_r',
alpha=0.1
);
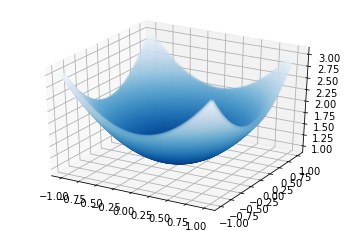
Далее устроим градиентный спуск для этого параметра k.
import tensorflow as tf
class ParameterFinder:
def __init__(self, initial):
self.k = tf.Variable(initial)
def predict(self, X, Y):
return X**2 + Y**2 + self.k ** 2
def mse(self, true, predicted):
return tf.reduce_mean(tf.square(true - predicted))
def update(self, X, Y, Z, alpha):
with tf.GradientTape(persistent=True) as tape:
loss = self.mse(Z, self.predict(X, Y))
dk = tape.gradient(loss, self.k)
self.k.assign_sub(alpha * dk)
return loss
def train(self, X, Y, Z, alpha=0.01, epochs=10, printable=True):
for epoch in range(epochs):
loss = self.update(X, Y, Z, alpha)
if printable:
print("Parameter %.3f" % self.k)
print('loss %.3f' % loss)
ParameterFinder(initial=4.0).train(data[:, 0], data[:, 1], data[:, 2], epochs=10)
Parameter 1.175
loss 0.185
ParameterFinder(initial=4.0).train(data[:, 0], data[:, 1], data[:, 2], epochs=100)
Parameter 1.000
loss 0.000
3. Немного о решающих деревьях¶
Деревья “плохи” тем, что их разделяющие границы - осепараллельны. Пример.
from sklearn.tree import DecisionTreeClassifier
np.random.seed(1)
data = np.column_stack([
np.random.uniform(-1, 1, size=50),
np.random.uniform(-1, 1, size=50)
])
classes = data[:, 1] > 0
plt.scatter(data[:, 0], data[:, 1], c=classes);
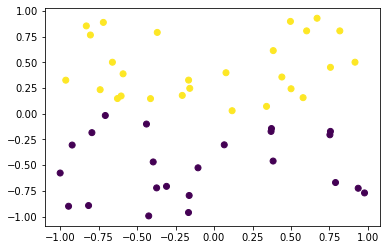
def plot_decisions(x, y, targets, classifier, labels=None):
x_min, x_max = x.min() - 1, x.max() + 1
y_min, y_max = y.min() - 1, y.max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01),
np.arange(y_min, y_max, 0.01))
z = classifier.predict(np.c_[xx.ravel(), yy.ravel()])
z = z.reshape(xx.shape)
c = plt.contourf(xx, yy, z, cmap='Paired', alpha=0.3)
for index in range(len(np.unique(targets))):
indices = np.where(targets == index)
plt.scatter(x[indices], y[indices], color=[
'b', 'r', 'y'
][index], label=labels[index] if labels is not None else index)
plt.legend()
plt.tight_layout()
plt.show()
classifier = DecisionTreeClassifier(max_depth=1, random_state=1).fit(data, classes)
plot_decisions(data[:, 0], data[:, 1], classes, classifier)
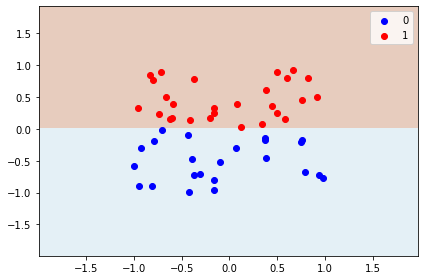
Это было ожидаемо, и решающее дерево по определению с такой простой задачей справилось. Что если мы повернем данные?
angle = np.deg2rad(45)
affine = np.array([
[np.cos(angle), -np.sin(angle)],
[np.sin(angle), +np.cos(angle)]
])
warped = np.array([
[
np.dot(affine[0], point),
np.dot(affine[1], point)
] for point in data
]).reshape(-1, 2)
classifier = DecisionTreeClassifier(max_depth=1, random_state=1).fit(warped, classes)
plot_decisions(warped[:, 0], warped[:, 1], classes, classifier)
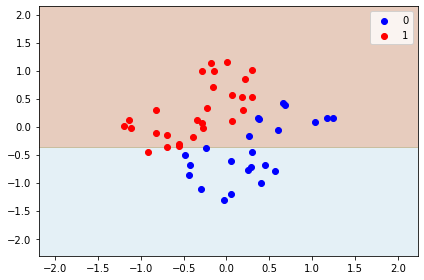
Граница уехала вниз, но теперь очевидно, большая ошибка. Что можно сделать? Давайте развернём их через PCA.
from sklearn.decomposition import PCA
reduced = PCA(n_components=2, random_state=1).fit_transform(warped)
classifier = DecisionTreeClassifier(max_depth=1, random_state=1).fit(reduced, classes)
plot_decisions(reduced[:, 0], reduced[:, 1], classes, classifier)
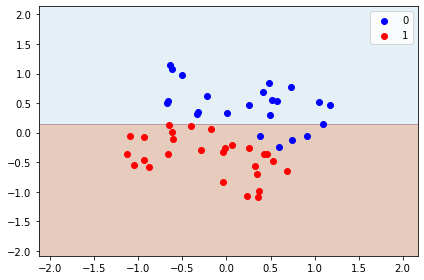
Лучше, как бы… но нет. Давайте использовать UMAP.
from umap import UMAP
mapped = UMAP(n_components=2, n_neighbors=30, random_state=1).fit_transform(warped)
classifier = DecisionTreeClassifier(max_depth=1, random_state=1).fit(mapped, classes)
plot_decisions(mapped[:, 0], mapped[:, 1], classes, classifier)
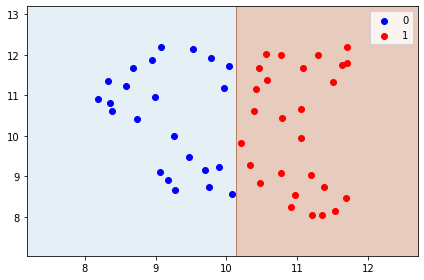
4. Топологический анализ¶
Или немного о том, как устроен UMAP.
Начинается всё слегка издалека: из топологии, раздела математики, который отвечает за различение объектов по связности - то есть сферу от бублика, или же восьмерку от кольца или окружности (попросту - числом “дырок” в связном множестве - многообразии). Объекты эквивалентны с точки зрения топологии, если у них количество этих самых “дырок” одинаково.
Наши же датасеты даны нам так называемым “облаком точек” в пространстве. Поскольку реальные данные не распределены равномерно по всему пространству - они же не шум, они даны нам на некоторой искривленной поверхности в пространстве, этаким подпространством которое может быть этим самым многообразием.
У нас же опять же - облако.
UMAP делает следущие вещи:
Берет и строит шары из каждой точки, используя ближайшие точки для определения радиуса шара, при этом чем дальше лежит точка от исходной, тем шар более “ослабевает” - то есть вводится некоторая локальная функция расстояния,
Шары, которые пересекаются - образуют некоторый граф, являющийся некоторым представлением интересующего нас многообразия. При этом связи (ребра) в графе - имеют вес, равный той самой метрике из пункта 1,
Веса на графе рассматриваются как некоторые вероятности существования ребра в этом графе (представляющем многообразие),
Далее в пространстве размерности пониже - ищется граф, который сохраняет эту же (вероятностную) структуру. Он и объявляется представлением исходного облака точек в пространстве пониженной размерности.
from sklearn.datasets import make_circles
from sklearn.preprocessing import StandardScaler
X1, y1 = make_circles(n_samples=100, noise=0.1, random_state=1, factor=0.25)
X2, y2 = make_circles(n_samples=100, noise=0.1, random_state=1, factor=0.25)
X2 = X2 * 3 + 10
X = np.row_stack([X1, X2])
y = np.row_stack([y1, y2]).flatten()
X = StandardScaler().fit_transform(X)
plt.scatter(X[:, 0], X[:, 1], c=y);

Параметр n_neighbors - указывает сколько соседей для каждой точки брать в рассмотрение. Чем он больше - тем глобальнее улавливаемое многообразие, то есть информация о мелких локальных “складках/сборках” теряется.
mapper = UMAP(n_components=2, n_neighbors=5).fit(X)
X_transformed = mapper.transform(X)
plt.scatter(X_transformed[:, 0], X_transformed[:, 1], c=y);

mapper = UMAP(n_components=2, n_neighbors=15).fit(X)
X_transformed = mapper.transform(X)
plt.scatter(X_transformed[:, 0], X_transformed[:, 1], c=y);

mapper = UMAP(n_components=2, n_neighbors=50).fit(X)
X_transformed = mapper.transform(X)
plt.scatter(X_transformed[:, 0], X_transformed[:, 1], c=y);

UMAP вполне подходит для задач:
Визуализации данных,
Инжиниринга признаков,
Препроцессинга табличных данных для кластеризации,
Препроцессинга векторов от нейросетей (для кластеризации или классификации).
Однако он может использоваться и в задачах обучения с учителем - то есть находить такие представления, которые хорошо разделяют классы.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, random_state=1, test_size=0.25
)
mapper = UMAP().fit(X_train, y_train)
X_transformed_train = mapper.transform(X_train)
plt.title('TRAIN')
plt.scatter(X_transformed_train[:, 0], X_transformed_train[:, 1], c=y_train);

X_transformed_test = mapper.transform(X_test)
plt.title('TEST')
plt.scatter(X_transformed_test[:, 0], X_transformed_test[:, 1], c=y_test);
